Introduction
As soon as a team selects a player in the draft, analysts rush to compare the player to historical players. Often, analysts draw these comparisons based off play style. After matching the play styles, analysts compare the prospect to a the best with that play style to give the prospect a ceiling. Fast and athletic point guard? Let’s compare him to Westbrook, Rose, and Wall. Long defender with a currently limited offensive game? Kawhi (looking at you, Chauncey Billups).
Though this method may be the easiest way for us to equate prospects to legends, it has its pitfalls. In Kawhi’s case, he developed a killer isolation game in the NBA, something we would have never seen coming at the time of the draft. Who would’ve thought Blake Griffin – a career 58.9% FT shooter in college – would grow to shoot 36.2% on 7 3-point attempts this year?
Players develop their play styles in different and unexpected ways. So, basing a comparison on an imagined reality where a player refines only his current skills seems odd. After all, we’re comparing them to what the stars became – not what they were when they came into the draft. Despite these issues though, this is often the best way to make comparisons for prospects.
To solve this issue, we can compare their college stats. Though comparing players based off similar stats won’t be perfectly accurate, it does give us some type of concrete metric for comparison. We’ll even find that many of these comparison players have similar play styles. Let’s draw comparisons for this year’s draft lottery.
Similarity metrics
There are many different metrics for measuring the distance between two sets of numbers, or vectors. In this post, we’ll use two metrics: cosine similarity and Euclidean distance.
Cosine similarity is the cosine of the angle that’s between two vectors. The vectors are cast into n dimensions, where n is the number of elements in the vectors.
This explanation of cosine similarity is not easy to understand. Instead, let’s do an example calculation of cosine similarity.
Let’s find the cosine similarity between the vector [.5, .5] and [1, .5]. The first step in calculating cosine similarity is taking the dot product of the two vectors, or multiplying the first element in each vector and adding it to the product of the second element in each vector. The dot product of the two vectors = .5 * 1 + .5 * .5 = .75.
Next, we’ll divide this dot product by the product of the length of each vector. The length of the vector = sqrt(x^2 + y^2).
The length of the first vector = sqrt(.5) = .707. The length of the second vector = sqrt(1.25) = 1.12. Altogether, we’ll do .75 / (sqrt(5) * sqrt(1.25)). For positive values, cosine similarity will be between 0 and 1; a cosine similarity of 1 indicates perfect similarity. After doing the above calculations, we can see that the cosine similarity for the two vectors is 0.95.
Euclidean distance is much, much simpler than cosine similarity. It’s an extension of the distance formula; the distance between (x1, y1) and (x2, y2) = sqrt((x2 – x1)^2 + (y2 – y1)^2).
Euclidean distance simply takes this distance formula and extends it for however many data points we have in each vector. Unlike cosine similarity, it is not bounded by a range. A Euclidean distance of 0 indicates perfect similarity.
Methods
First, I created a data base of the college advanced and counting stats for every lottery pick in this year’s draft. For the historical data set, I collected college stats for every lottery pick who played in college since 1990. The restriction is set at 1990 because players drafted in 1990 played their entire college careers with a 3-point line. All data is from Sports-Reference.
Though the NBA did not always have 30 teams – meaning the lottery was not always the top 14 picks – I define “lottery” as the top 14 given that’s what it is today. Because the data set only includes college players, if an overseas player was selected in the top 14, then the 15th pick is considered in the lottery given that he’s among the top 14 NCAA players.
For these players, I ended up using the following stats in the similarity vectors:
| Counting stats | Defensive stats | Advanced stats |
|---|---|---|
| G | STL | TS% |
| PTS | BLK | 3PAr |
| AST | PF | FTr |
| TRB | WS | |
| TOV |
All the counting and defensive stats were adjusted to be per-40 stats. Because we ended up using win shares, which is only available for players since the 1996 draft, we’ll only compare this year’s lottery to all lotteries since 1996. All stats were also standardized to be between 0 and 1 for the purpose of the similarity metrics.
For each rookie, we computed cosine similarity and Euclidean distance to every player in the historical database. We then analyzed the top-5 most similar players returned by each metric.
Inspiration
This post is inspired by u/kip_chelly’s post on Reddit a couple years ago. He also used cosine similarity to compare draft prospects to previous top-5 picks and stars. It is an excellent post that produced some interesting results that we can look back at; it’s a highly recommended read.
I’ve expanded on his post by adding Euclidean distance and using fewer dimensions (stats), making for a simpler comparison. The only issue with his excellent analysis is that his historical data set included primarily good players, so everyone would be compared to stars. I’ve expanded on this part too by using every lottery player and comparing their college careers instead of individual seasons.
Results
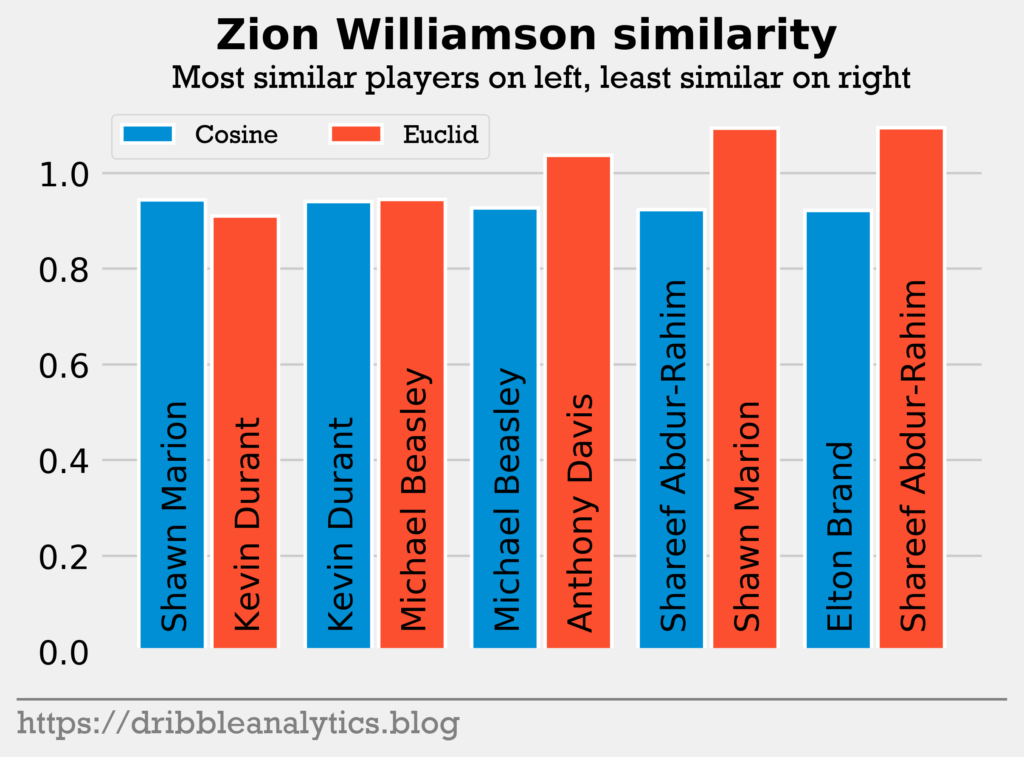
Pick 1: Zion Williamson. Far and away the top prospect in the 2019 draft, Zion Williamson often draws comparisons to Charles Barkley and Blake Griffin. He had the lowest Euclidean distance to Kevin Durant and the highest cosine similarity to Shawn Marion. Though Marion appears to be an unflattering comparison given Zion’s lofty expectations, Marion was a 4x All-Star, 2x All-NBA player, and an NBA champion with the Mavs in 2011.
Barkley is not included in the database, meaning Zion could not be compared to him. Surprisingly, Blake Griffin was not among Zion’s top comparisons. Griffin had the 7th lowest Euclidean distance and only the 18th highest cosine similarity to Zion. Looking at their college stats, threes and free throws were likely the biggest difference. Blake Griffin’s free throw rate was about 1.5x higher, while his 3-point attempt rate was about 12 times lower.
Zion was the only player to have Anthony Davis in his top-5 most similar players. He and R.J. Barrett were the only players to return Kevin Durant as one of their most similar players.
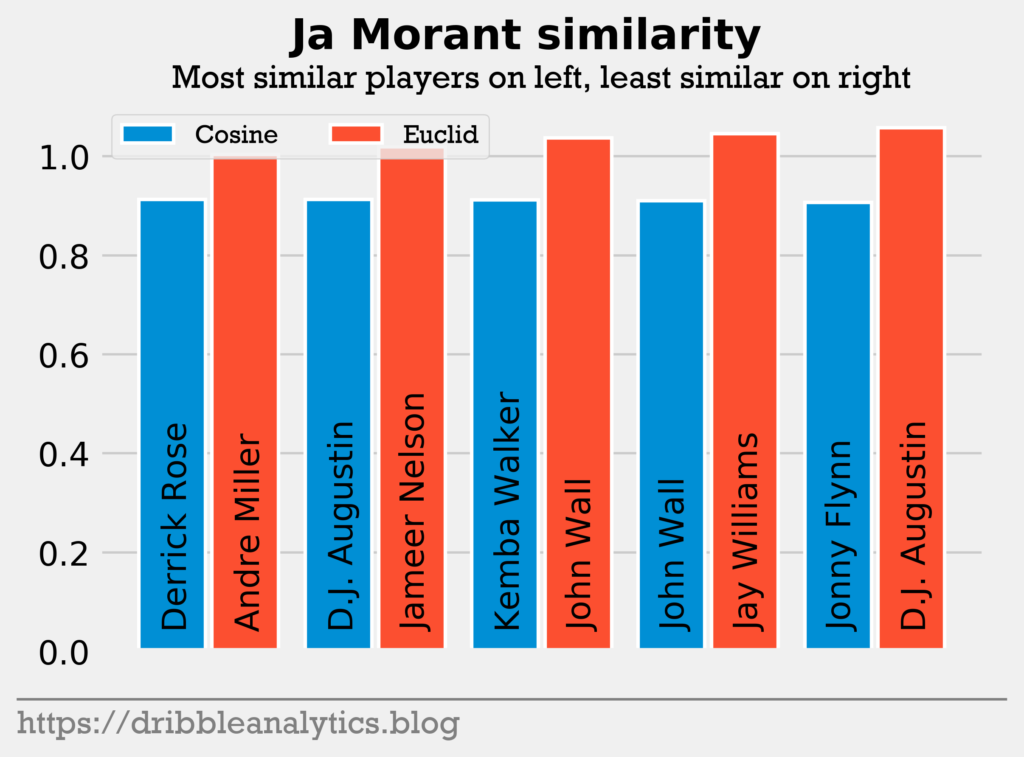
Pick 2: Ja Morant. The top point guard in this draft, Ja Morant’s mix of athleticism and passing ability leads many to compare him to John Wall. Indeed, Morant was the only player to return John Wall. His highest cosine similarity was to Derrick Rose – another common comparison. Andre Miller – who lead the league in assists in just his third year – had the lowest Euclidean distance to Ja Morant.
In this case, the statistical comparison matches the typical play style comparison, as Morant returned both Wall and Rose. Though Miller was not as athletic as Morant, he was an excellent distributor. This sheds light on Morant’s potential as a distributor.
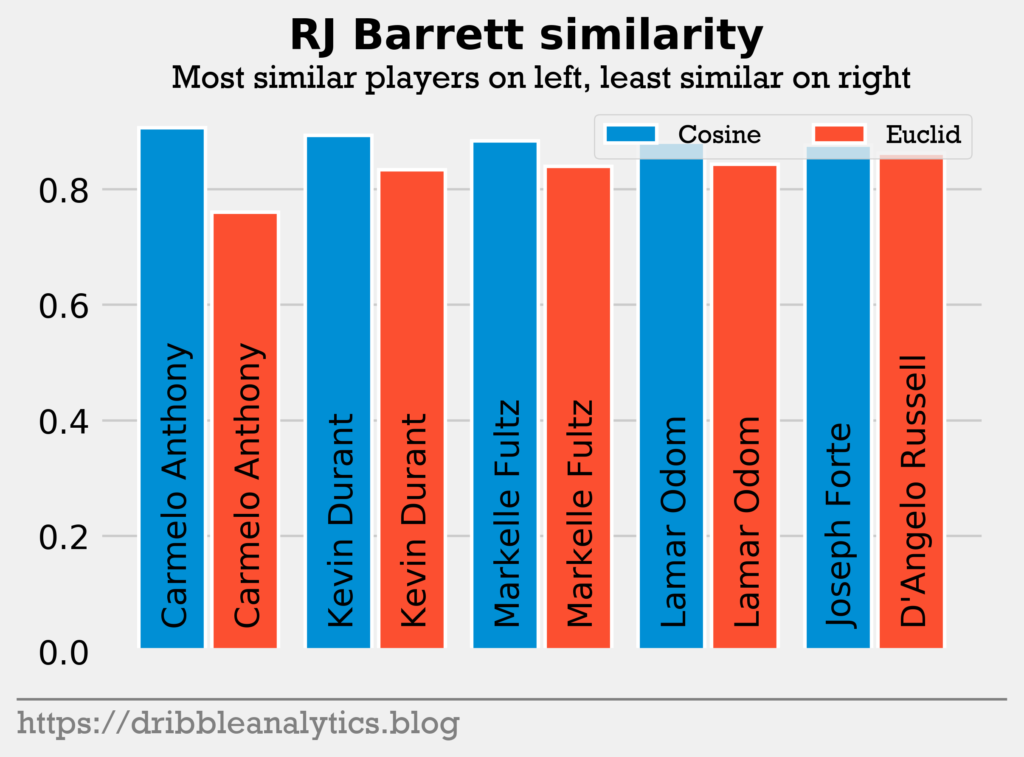
Pick 3: R.J. Barrett. A smooth ball handler and mid-range shooter, R.J. Barrett was most similar to Carmelo Anthony in both cosine similarity and Euclidean distance.
Barrett was the only player to return Melo, making the comparison appear even stronger. Barrett also returned Markelle Fultz and D’Angelo Russell; both came out of college as smooth guards with excellent potential to score all over the floor. Highlighting his ball handling and transition abilities, we found that Barrett was also the only player to return Lamar Odom.
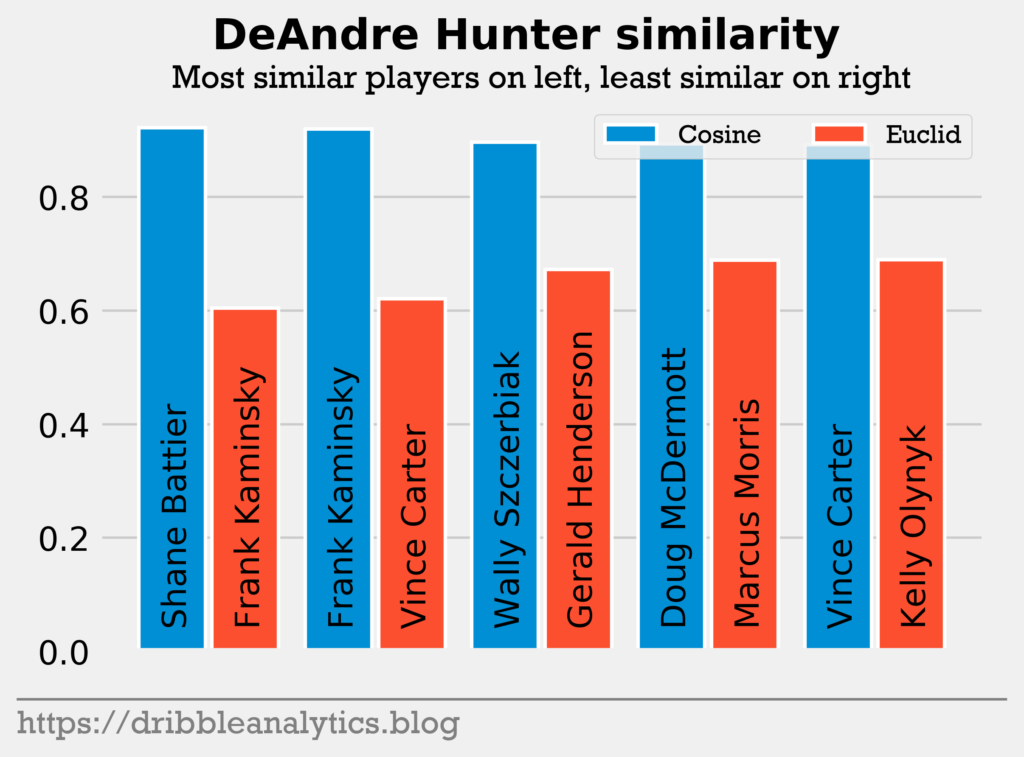
Pick 4: DeAndre Hunter. A defensive stud with excellent 3&D potential, DeAndre Hunter had the highest cosine similarity to Shane Battier. He had the lowest Euclidean distance to Frank Kaminsky. Both players had excellent defensive stats on high efficiency in college.
Surprisingly, Hunter was the only player to return Vince Carter. Hunter’s combination of excellent defense and shooting makes him one of the most NBA-ready prospects in the draft. Unfortunately, this combo leads to some disappointing comparisons.
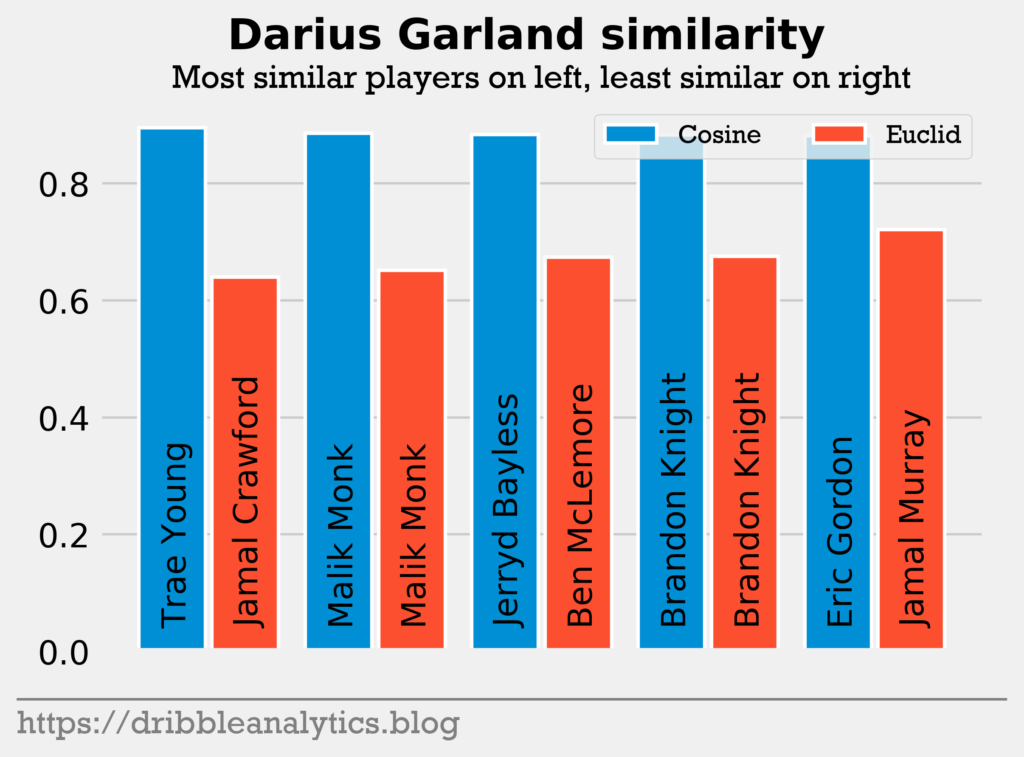
Pick 5: Darius Garland. The second point guard off the board after Morant, Darius Garland has drawn comparisons to Damian Lillard given his range and scoring ability. Garland had the highest cosine similarity to Trae Young. He had the lowest Euclidean distance to Jamal Crawford.
Though Garland seems much more athletic than Young, the comparison seems fair given the mix of pull-up shooting and distribution.
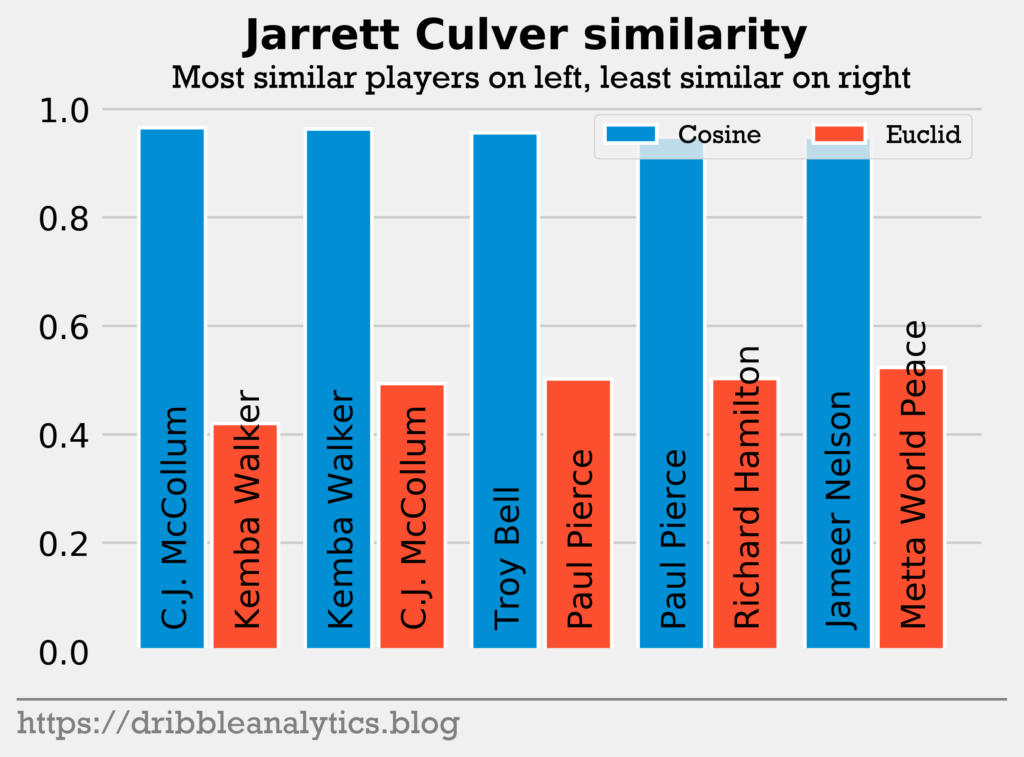
Pick 6: Jarrett Culver. One of the most versatile wings in the draft, Jarrett Culver had the highest cosine similarity to C.J. McCollum. Though he is 3 inches taller and has a 3.5 inch longer wingspan, Culver has shown flashes of McCollum’s well-rounded guard skill set. Culver was the only player to return McCollum.
Interestingly, both of Culver’s closest comparisons were guards; he had the lowest Euclidean distance to Kemba Walker. In addition to returning these two excellent guards, Culver was the only player to return Paul Pierce.
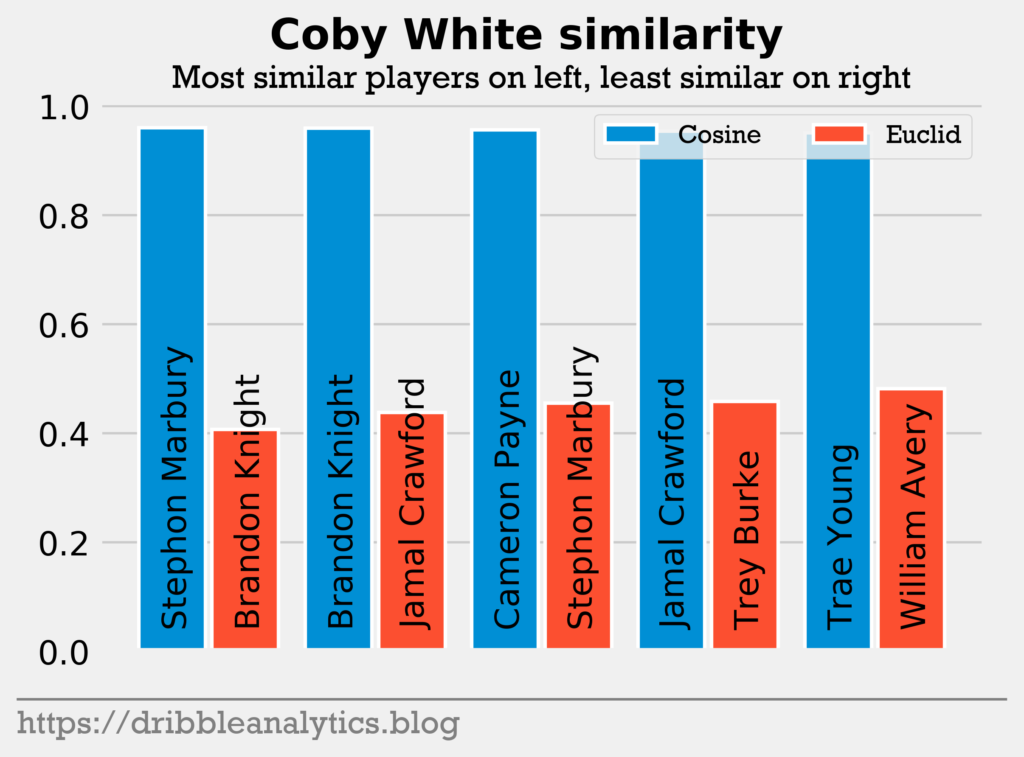
Pick 7: Coby White. A true speed demon, Coby White had the highest cosine similarity to Stephon Marbury. He had the lowest Euclidean distance to Brandon Knight.
This seems like an excellent comparison given that Marbury also liked to play a fast game. Both White and Marbury averaged under 5 assists per game in college. It seems the NBA spacing and speed helped Marbury, as he average 15.8 points and 7.8 assists per game as a rookie.
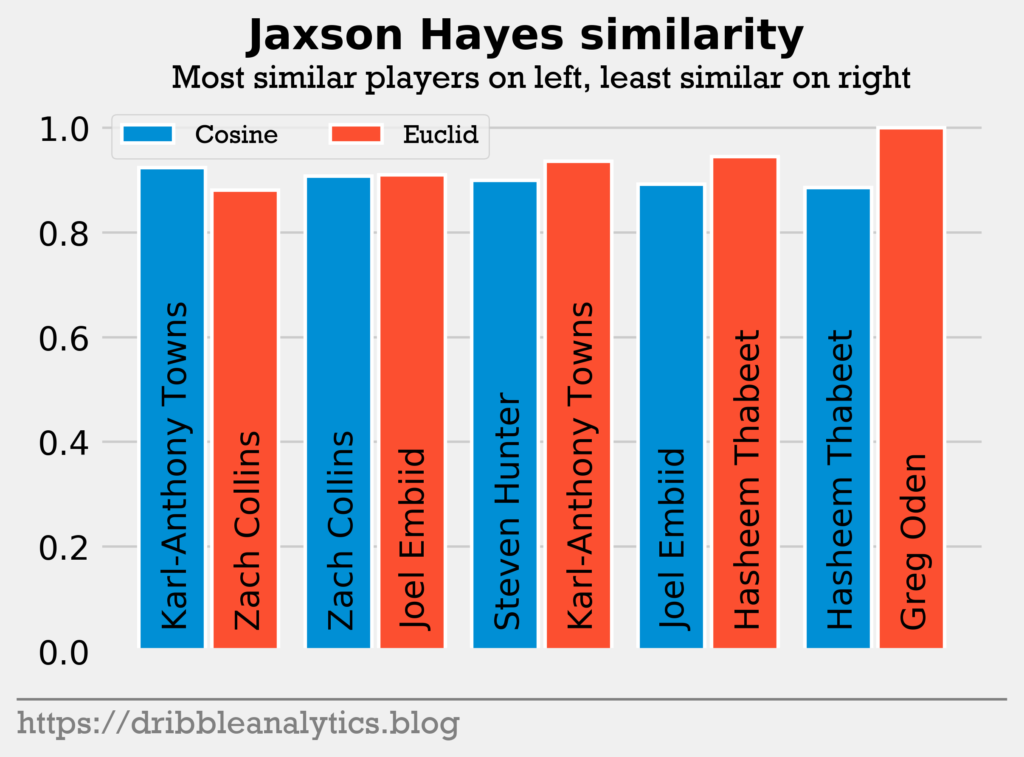
Pick 8: Jaxson Hayes. Jaxson Hayes was the first true rim-protecting big off the board. In college, he was a quick rim-running big, making the likes of Clint Capela a natural comparison. However, unlike Capela or DeAndre Jordan, Hayes shot an excellent 74% from the free throw line.
Hayes had the highest cosine similarity to another player who appeared to be a defensive big, but shot well from the free throw line in college: Karl-Anthony Towns. Though Hayes isn’t nearly as polished offensively as Towns – who showed flashes of being a great passer and mid-range shooter – was coming out of college, the comparison is encouraging. He had the lowest Euclidean distance to Zach Collins. Further strengthening his potential, Hayes was the only player to return Karl-Anthony Towns and Joel Embiid.
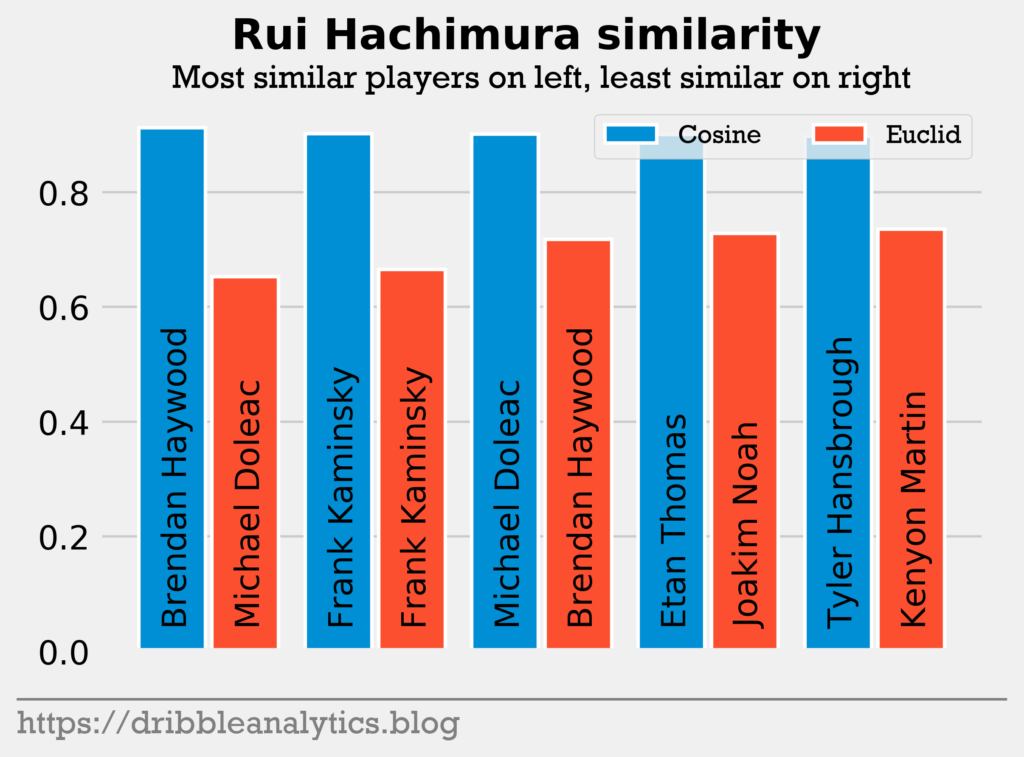
Pick 9: Rui Hachimura. Rui Hachimura progressed very well while at Gonzaga. His freshman year, he barely saw the court, playing only 4.6 MPG. However, this year, he scored 19.7 PPG on high efficiency. He has excellent potential as a combo forward. However, his comparisons are not as noticeable as some of the players before him. Interestingly, Hachimura was primarily compared to centers.
Hachimura had the highest cosine similarity to Brendan Haywood. Haywood had a 14-year career as an inside center. He was a role player for the Mavs in their championship season and was top-5 in the league in blocks in the 2009-2010 season. Hachimura had the lowest Euclidean distance to Michael Doleac, another center. He was the only player to return Joakim Noah.
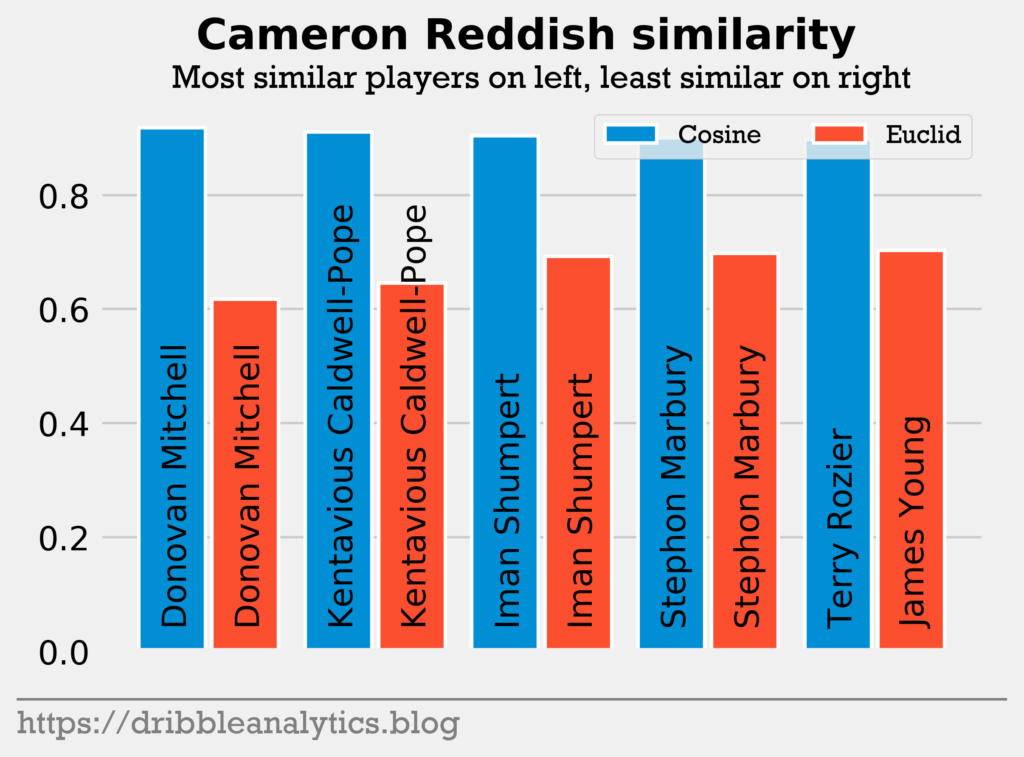
Pick 10: Cam Reddish. Playing alongside Zion Williamson and R.J. Barrett, Cam Reddish had little opportunity to shine at Duke. However, he appears to have the potential of a star scorer.
Reddish had the highest cosine similarity and lowest Euclidean distance to Donovan Mitchell. He was the only player to return Mitchell. Like Mitchell, Reddish may greatly benefit from the spacing and opportunity for him in the NBA.
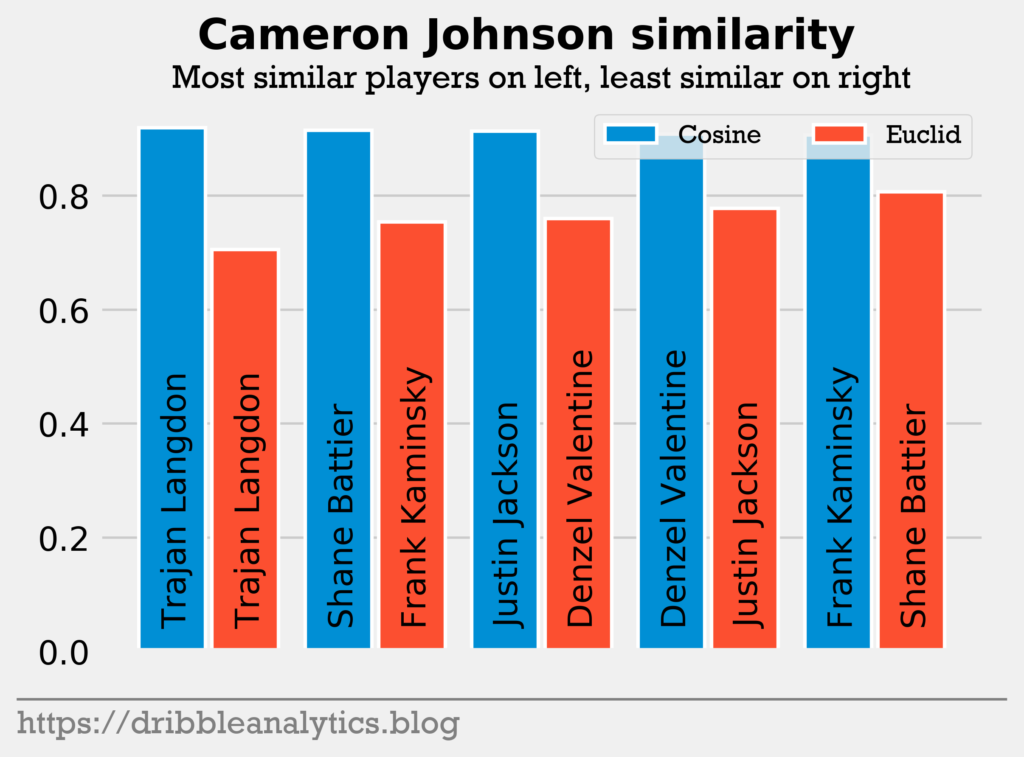
Pick 11: Cam Johnson. Cam Johnson seemed to be a reach according to many analysts. Though he was projected to go in the late first-round, the Suns took him 11th overall. Nevertheless, Johnson has excellent potential to be a productive 3&D forward.
Johnson had the highest cosine similarity and lowest Euclidean distance to Trajan Langdon, a prolific shooter from Duke. Langdon played in the NBA for 3 seasons before having a great career in Europe. Today, Langdon is the GM of the Pelicans. Johnson was the only player along with DeAndre Hunter to return Shane Battier.
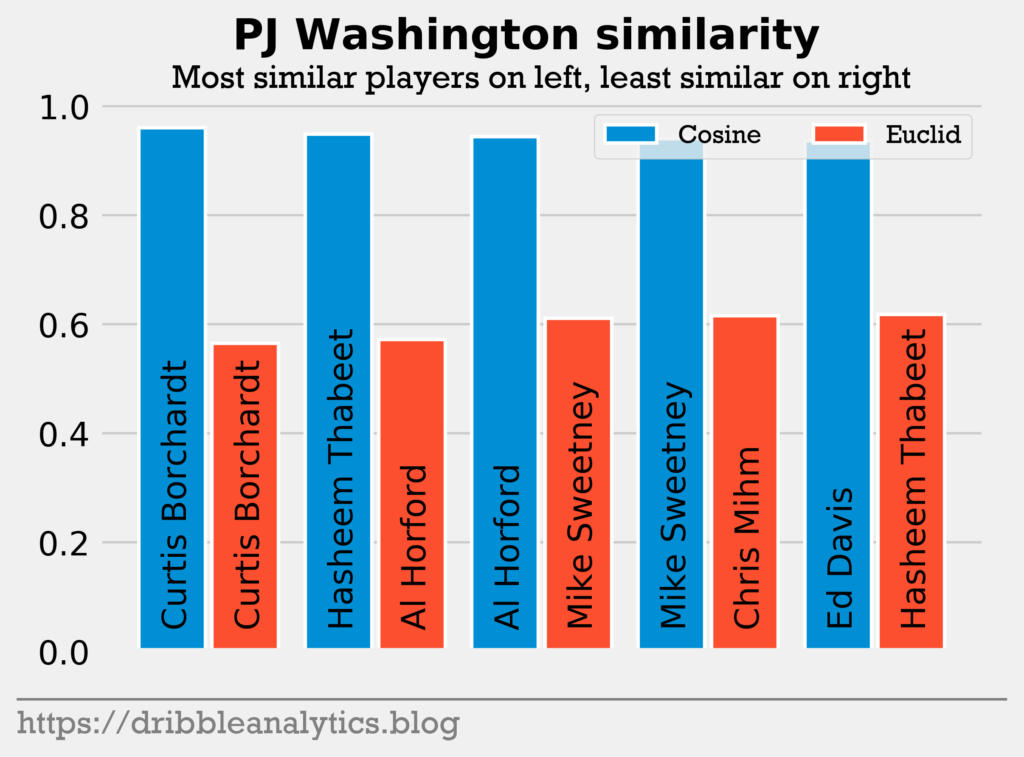
Pick 12: P.J. Washington. A great versatile big, P.J. Washington had the highest cosine similarity and lowest Euclidean distance to Curtis Borchardt. Borchardt played for the Jazz for 2 seasons before being traded and then going to play in Europe. The 2002 draft had 6 players who didn’t play in college before Borchardt, so he was not actually picked in the lottery, but was moved up to “lottery status” for this analysis. However, to compare Washington to players picked in the lottery, we’ll look at the second best comparisons.
Washington had the second highest cosine similarity to Hasheem Thabeet and the second lowest Euclidean distance to Al Horford. Horford seems to be a bast-case comparison for Washington in terms of refining his passing and scoring while becoming a great defender. Washington was the only player to return Al Horford.
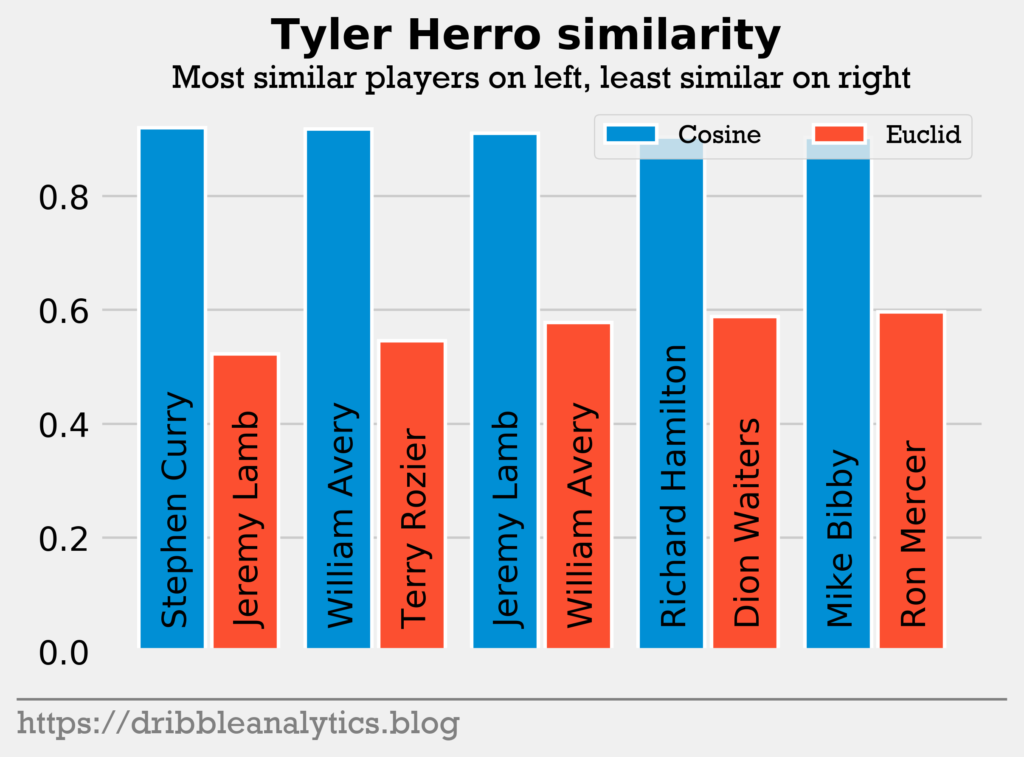
Pick 13: Tyler Herro. One of the best pure shooters in the draft, Tyler Herro had the highest cosine similarity to Steph Curry and lowest Euclidean distance to Jeremy Lamb. He was the only player to return Curry.
Though it’s clearly unfair to compare Herro to the greatest shooter ever, Herro seems to have many of Curry’s qualities. Herro is an excellent shooter off the dribble, an intelligent player off the ball, and has a quick release.
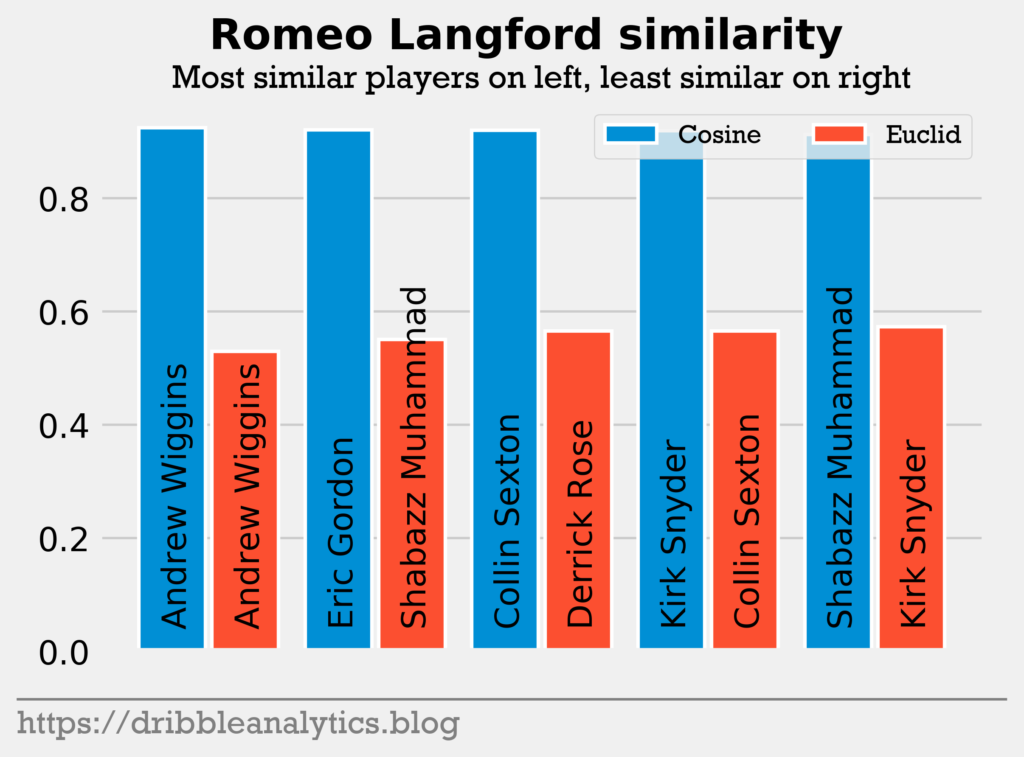
Pick 14: Romeo Langford. The final player in the lottery, Romeo Langford had the highest cosine similarity and lowest Euclidean distance to Andrew Wiggins. Like Wiggins, Langford seems to be a smooth slashing wing. Unfortunately, Langford seems to have a similar demeanor to Wiggins. NBADraft.net lists Langford’s first weakness as “doesn’t always look fully engaged in the game and intensity level seems to come and go.”
Along with being the only player to return Andrew Wiggins, Langford was the only player aside from Ja Morant to return Derrick Rose.