Is wingspan or height a better predictor of NBA defense?

Summary: Though not all regressions were statistically significant, every regression showed that wingspan is more correlated with better defense than height.

Introduction

With the increasing focus on positionless basketball, switching on defense has become more important. Maintaining a high-quality defense requires not only the quickness and strength for bigs to be able to defend guards and vice versa, but also the wingspan to be able to attack close outs and disrupt passing lanes. One of the leaders of this positionless revolution, Bob Myers, GM of the Warriors, explained that his ideal player “would be 6-foot-8 with a 7-foot-6 wingspan and still be able to shoot.”^[1] After all, players contest shots and intercept passes with their arms – not their heads. So, it would make sense to value wingspan over height when evaluating a prospect’s defensive potential.

For example, watch how Rudy Gobert guards Deron Williams on this play:

Williams has a step on Gobert, and goes for the reverse, which should give him an easier shot. However, Gobert recovers and blocks the shot due to his wingspan.

Aside from blocking shots, a longer wingspan allows a defender to deflect more passes. Watch how Kawhi Leonard can get the steal here on the low bounce pass:

Other factors such as hustle, strength, and coaching affect defense. Even though individual defensive stats such as defensive win shares are flawed because they are often dependent on factors out of the player’s control, we can use these statistics to gauge a player’s defensive ability. On a team-by-team basis, we can use defensive rating to evaluate the team’s defense.

With these stats, we can get a rough idea of a team or player’s defensive ability. By comparing this to both wingspan and height, we can find the importance of each. Is wingspan or height more correlated to these defensive metrics? Even if one is more correlated than the other, is the relationship statistically significant such that we can say which is a better predictor of defense?

Methods

First, I created a database of the height and wingspan of all 540 players who received any playing time this year. The data can be downloaded on my Github here.

On a player-by-player basis, I compared the measurements to their defensive win shares (DWS – higher is better). After examining the correlation for all NBA players, I split up the data into guards, forwards, and centers so that the data has more context (as classified by Basketball Reference). For example, in a full-league analysis, great defensive guards could be major outliers, especially given that bigmen often have higher DWS.

On a team-by-team basis, I compared each team’s wingspan and height to its defensive rating, or points allowed per 100 possessions (DRTG). I used a minutes-weighted average of wingspan and height such that the data accurately represents the team’s measurements

Assuming both regressions are statistically significant (p-value < 0.05), we can conclude that whichever regression returned a higher correlation coefficient (Pearson’s r) is a better predictor of NBA defense.

Without a p-value < 0.05, we can speculate whichever has the higher coefficient may be a better predictor of defense, but the null hypothesis (that wingspan/height is not related to defense) cannot be rejected.

Note that a higher DWS is better, so the factor with a greater r-value (correlation coefficient) is a better predictor of DWS. However, a lower DRTG is better, so the factor with a more negative r-value is a better predictor of DRTG.

What We’re Looking For

To determine which factor is a better predictor of defense, we’ll look at their r-values. The statistical significance threshold is importance, because we can’t reject the null hypothesis (that neither wingspan nor height predict defense) without statistical significance. So, without p-value < 0.05, the r-value differences are significantly less important.When the results are statistically significant, we can compare the wingspan and height correlations’ r-values. Note that we’re comparing the r-values of the wingspan and height regressions to each other. So, while a low r-value shows that one factor is not a great predictor of defense, we care about whether that factor has a higher r-value than the other.

Results: All Players

The two graphs below show the wingspan and height vs. DWS for all 540 NBA players who received any playing time this year.

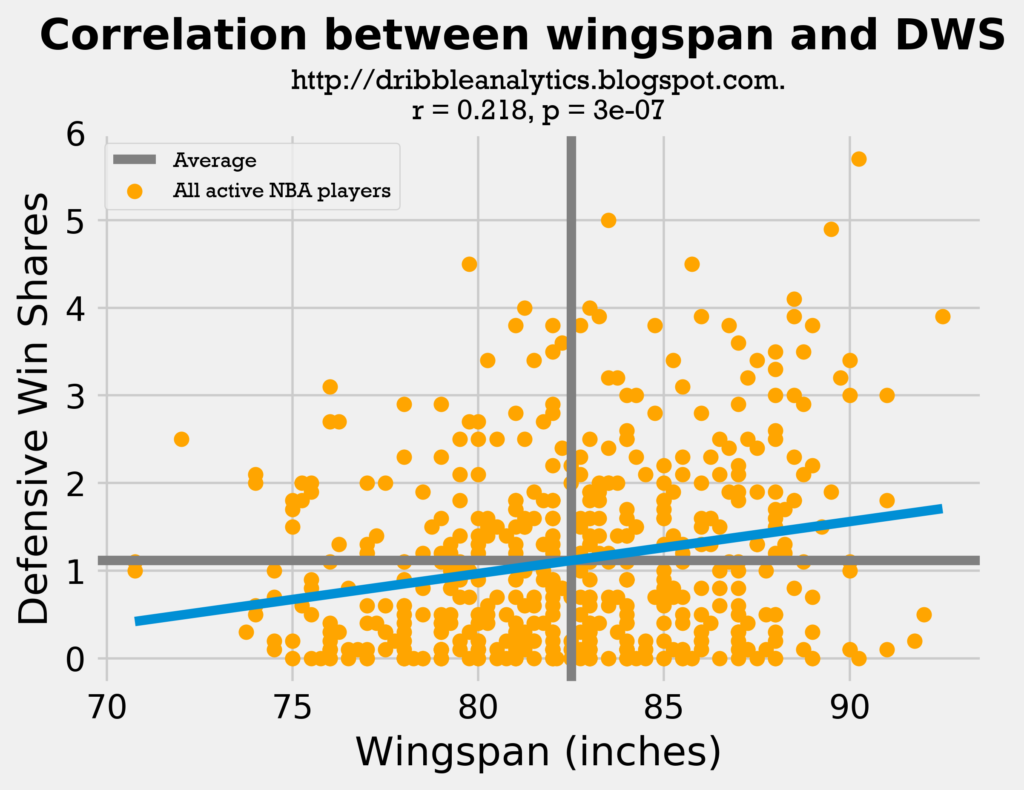
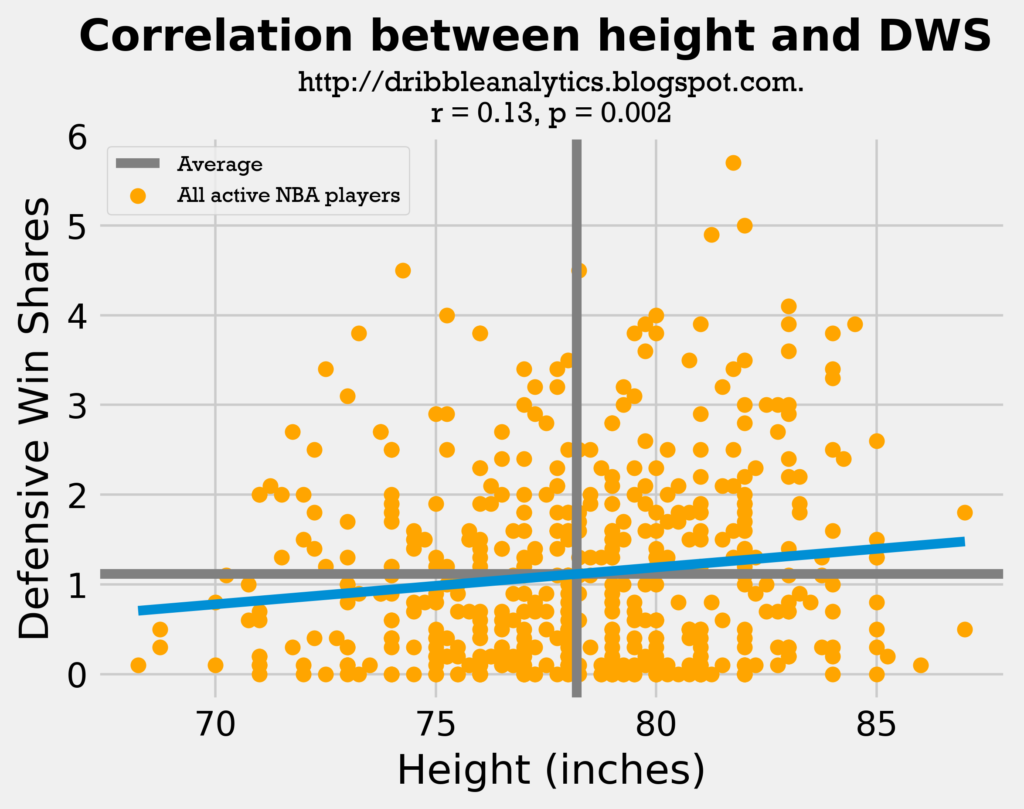
The correlation coefficient between wingspan and DWS is 0.218, while the coefficient between height and DWS is only 0.13. Both regressions were statistically significant, with the wingspan regression being much more so. Using an exponential trendline here may give even more context to the relationships.

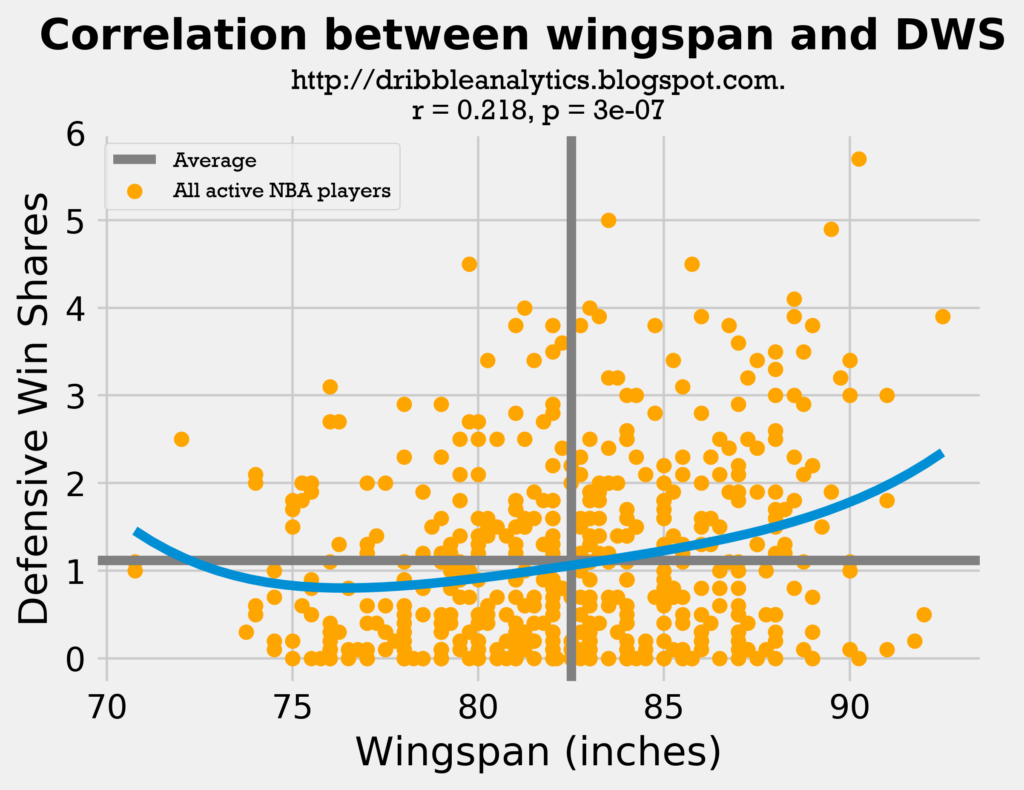
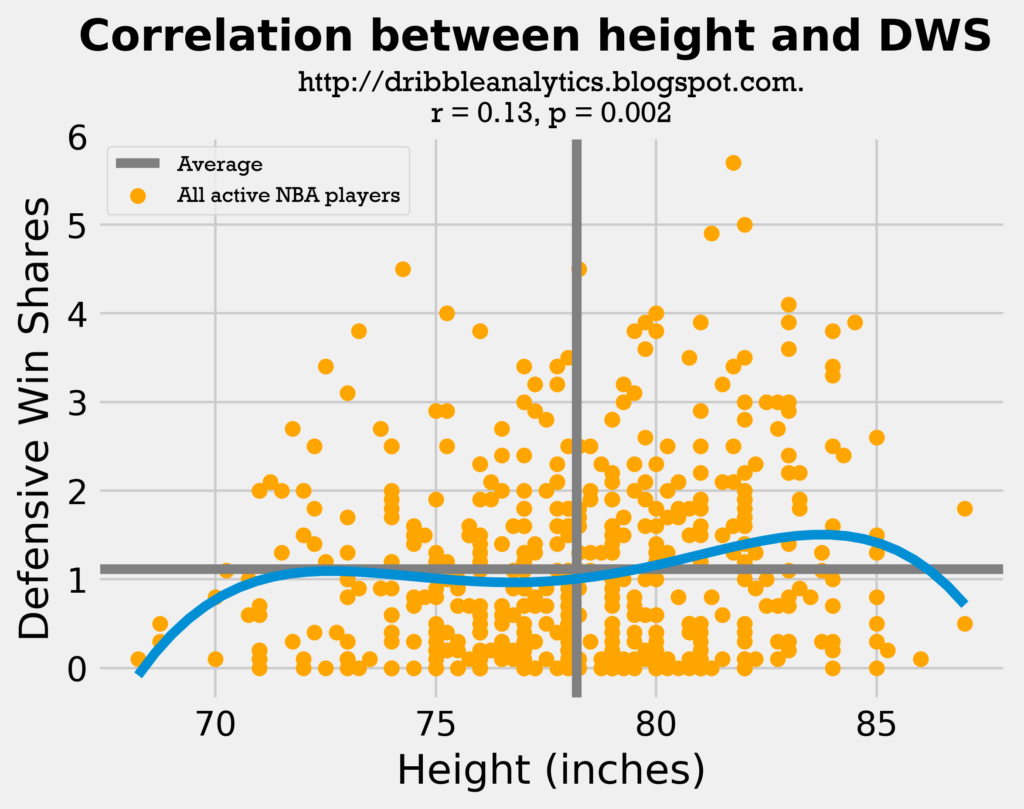
The exponential trendline for height shows two important things:

1. Very short guards have essentially no chance of being effective defenders (…Isaiah Thomas)
2. A taller defender is not necessarily better, as seen by the dip in the trendline around the average height. The wingspan trendline has no such dip; it consistently rises after the players with the shortest wingspans (quick guards).

Summary:

• Wingspan: correlation coefficient = 0.218, p-value = 3e-07 (0.0000003; statistically significant)
• Height: correlation coefficient = 0.130, p-value = 0.002 (statistically significant)

Results: Guards

The following two graphs show wingspan and height vs. DWS for all point guards and shooting guards.

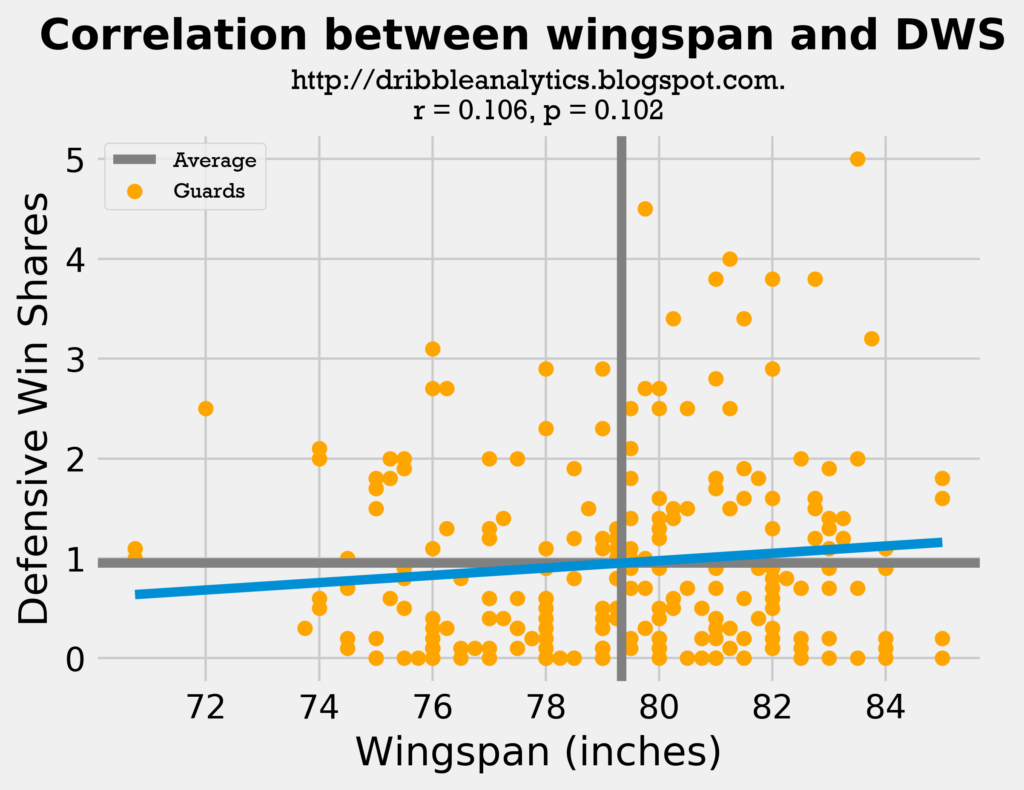
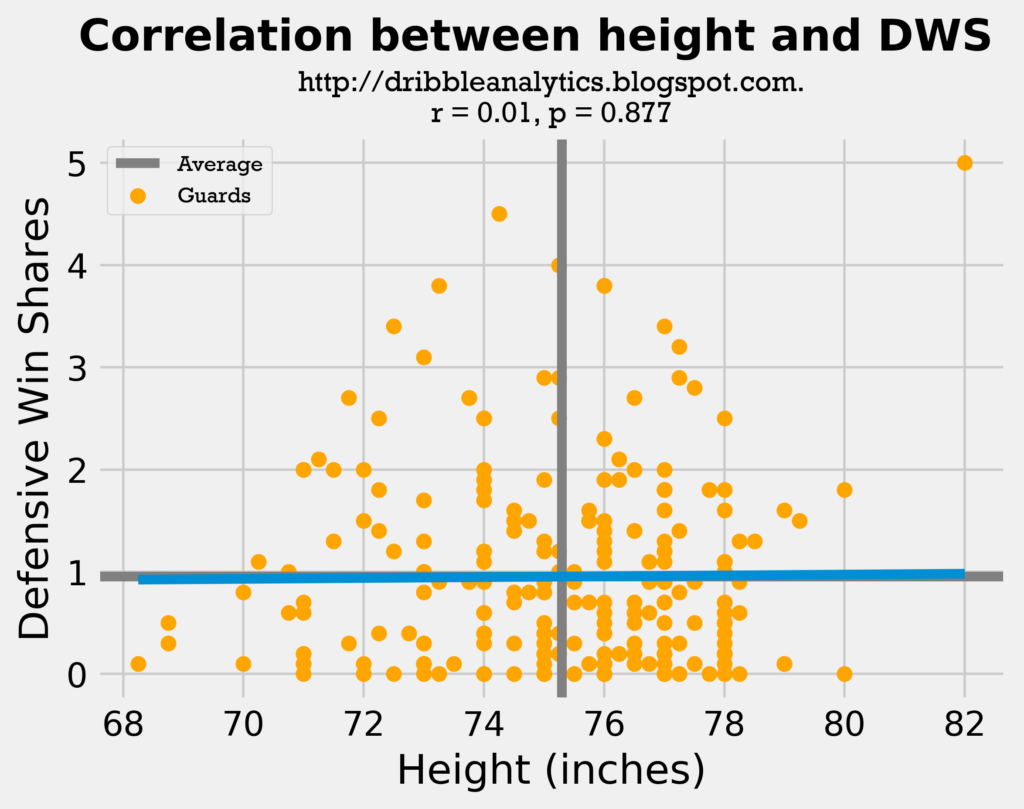
Although neither regression was statistically significant, the wingspan vs. DWS had both a higher r-value (0.106 vs. 0.010) and a lower p-value (0.102 vs. 0.877) than the height vs. DWS regression.

The results were not statistically significant, probably because guards have a broader range of wingspans and heights than other positions. This can be seen in the exponential trendlines; notice the massive rise at the right-most end of the height trendline because of Ben Simmons.

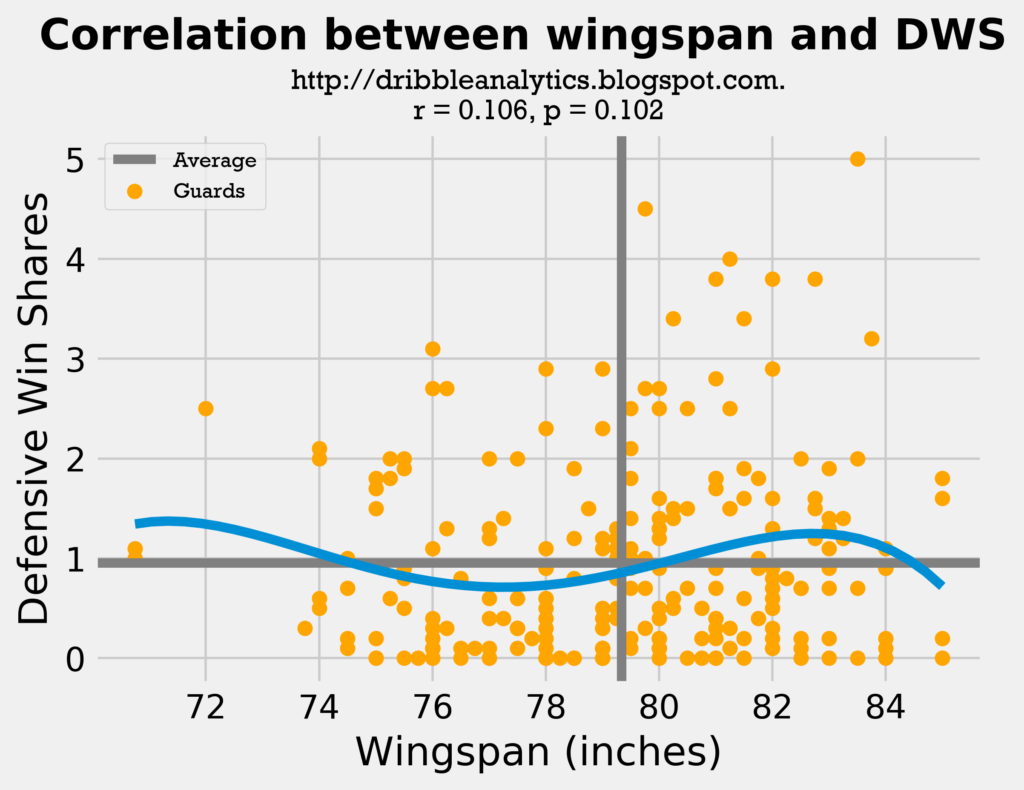
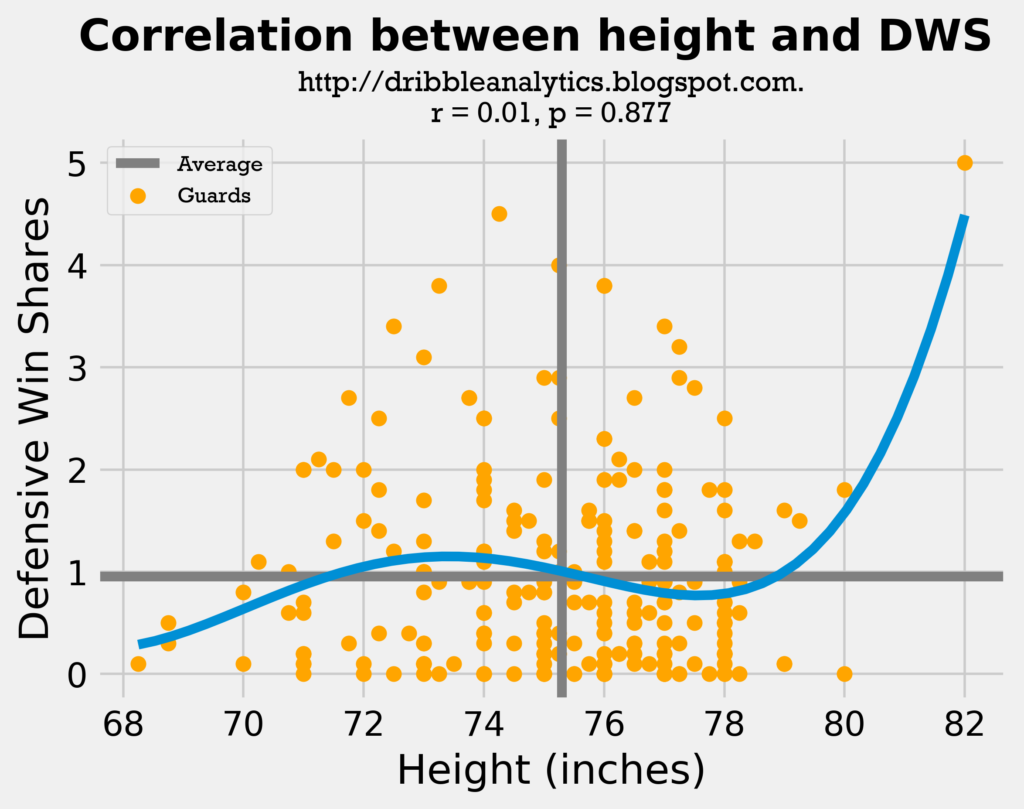
This exponential trendline shows that there are two groups of very effective defensive guards:

1. Middling wingspan guards, who are probably great defenders because of their quickness (like Chris Paul).
2. Long wingspan guards, who are probably great defenders because they can contest shots, interrupt passing lanes, and swipe at defenders more easily (like Ricky Rubio).

In terms of height, there isn’t really a common trend – the sharp rise at the end is solely because of Ben Simmons.

Summary:

• Wingspan: correlation coefficient = 0.106, p-value = 0.102 (not statistically significant)
• Height: correlation coefficient = 0.010, p-value = 0.877 (not statistically significant)

Results: Forwards

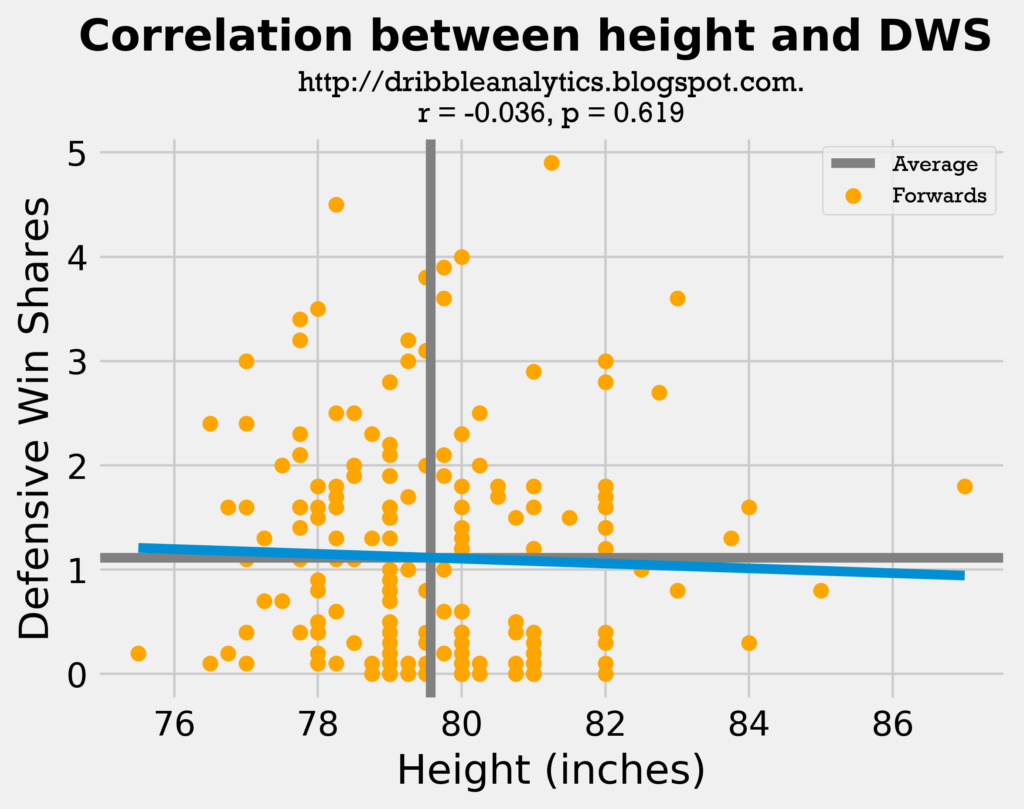
The following two graphs show wingspan and height vs. DWS for all small forwards and power forwards.

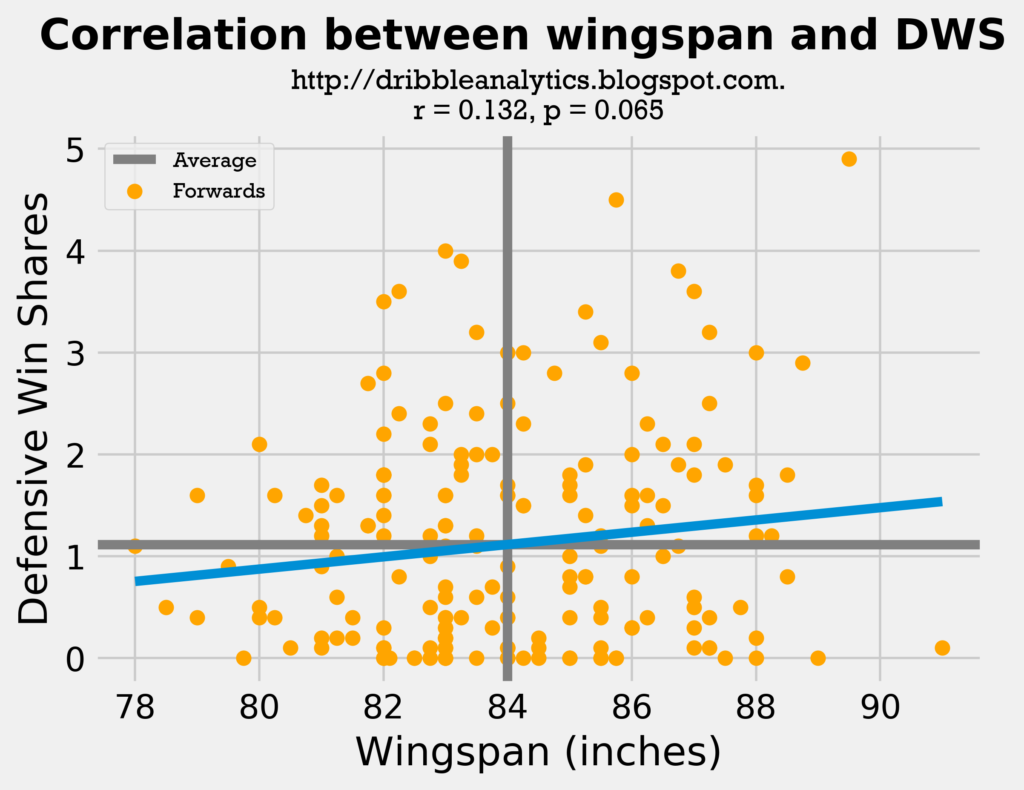
Though neither regression is statistically significant (the wingspan one is very close at a p-value of 0.065, but I use p-value < 0.05 for significance), this regression really shows the importance of wingspan in switching. I would imagine that forwards are involved in the most defensive switching, probably followed by centers (switching on the P&R onto guards) and then guards (rarely switch on to bigmen); forwards are expected to be able to keep up with guards and body up big men.  

Because of this expectation, the regression supports that wingspan is crucial (despite it’s lack of statistical significance). Wingspan had a correlation coefficient of 0.132. While not high, this is special considering height had a correlation coefficient of -0.036. Essentially, height had no correlation to DWS among forwards – it even had a negative one, maybe because bigger forwards are less mobile.

This is supported by the fact that the exponential trendline for wingspan mostly increases, while the exponential trendline for height fluctuates.

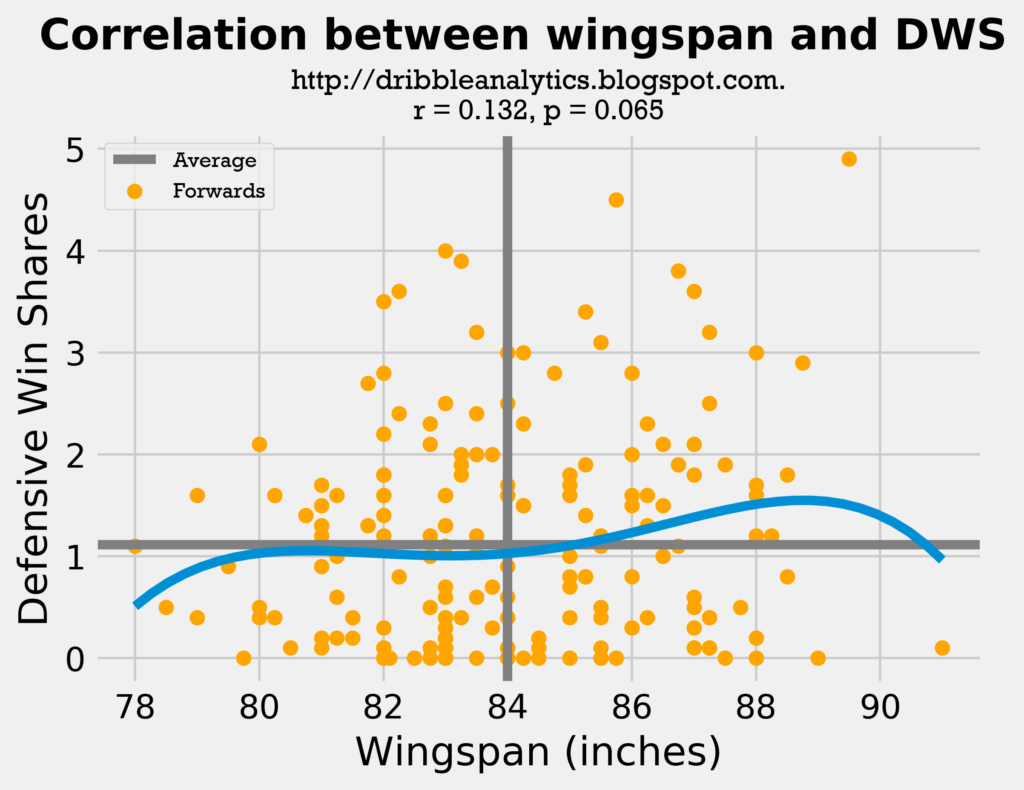
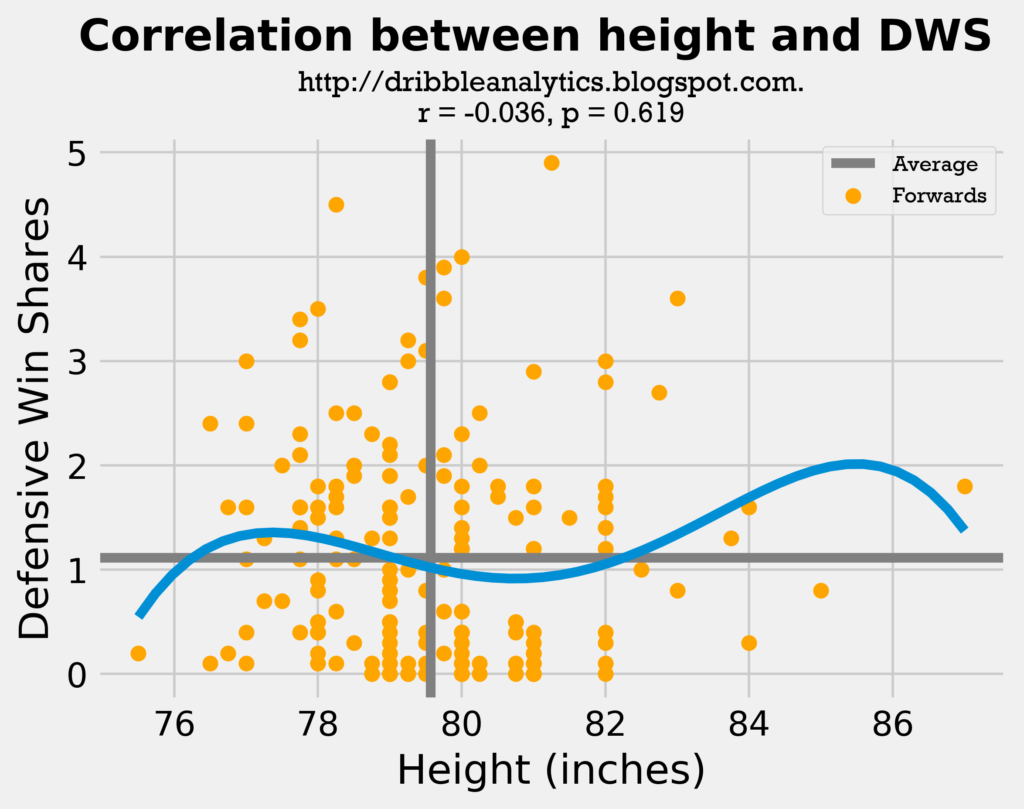
The exponential wingspan trendline stays mostly consistent for the forwards with a near-average wingspan, and then rises for those with an above-average wingspan. At the right-most end, the trendline falls, but this is completely due to Bruno Caboclo and his 7′ 7” wingspan.

Summary:

• Wingspan: correlation coefficient = 0.132, p-value = 0.065 (not statistically significant, but pretty close)
• Height: correlation coefficient = -0.036, p-value = 0.619 (not statistically significant)

Results: Centers

By far the most compelling results are obtained from the centers regression. The following two graphs show wingspan and height vs. DWS for all centers.

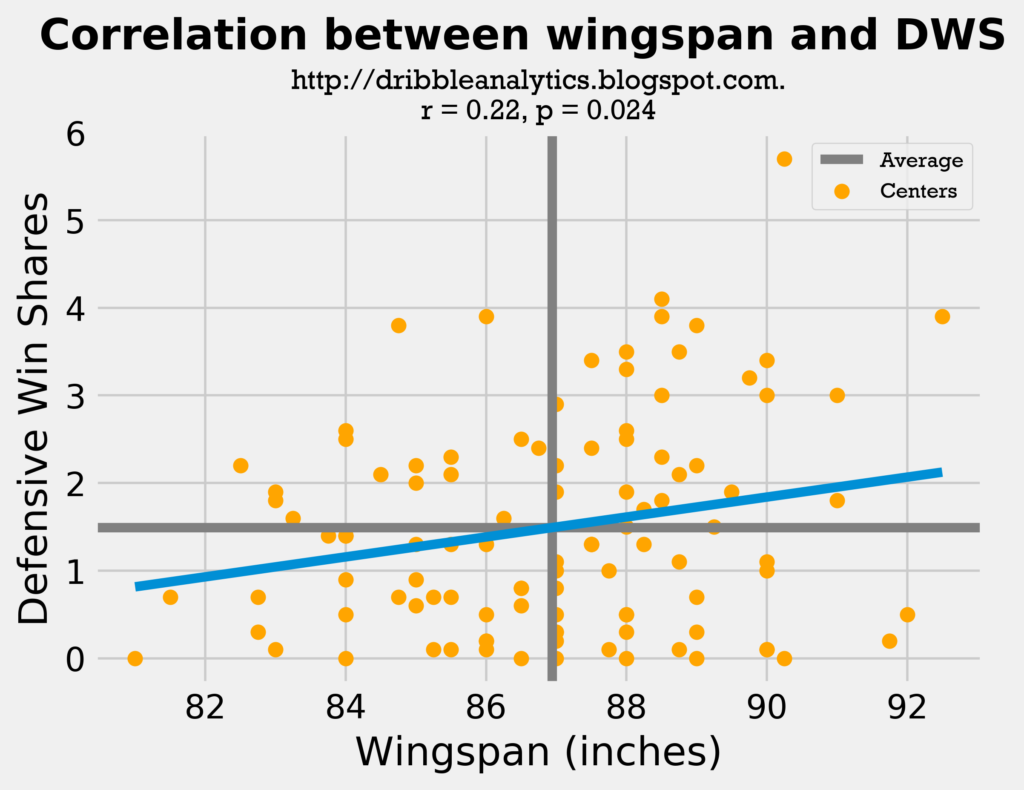
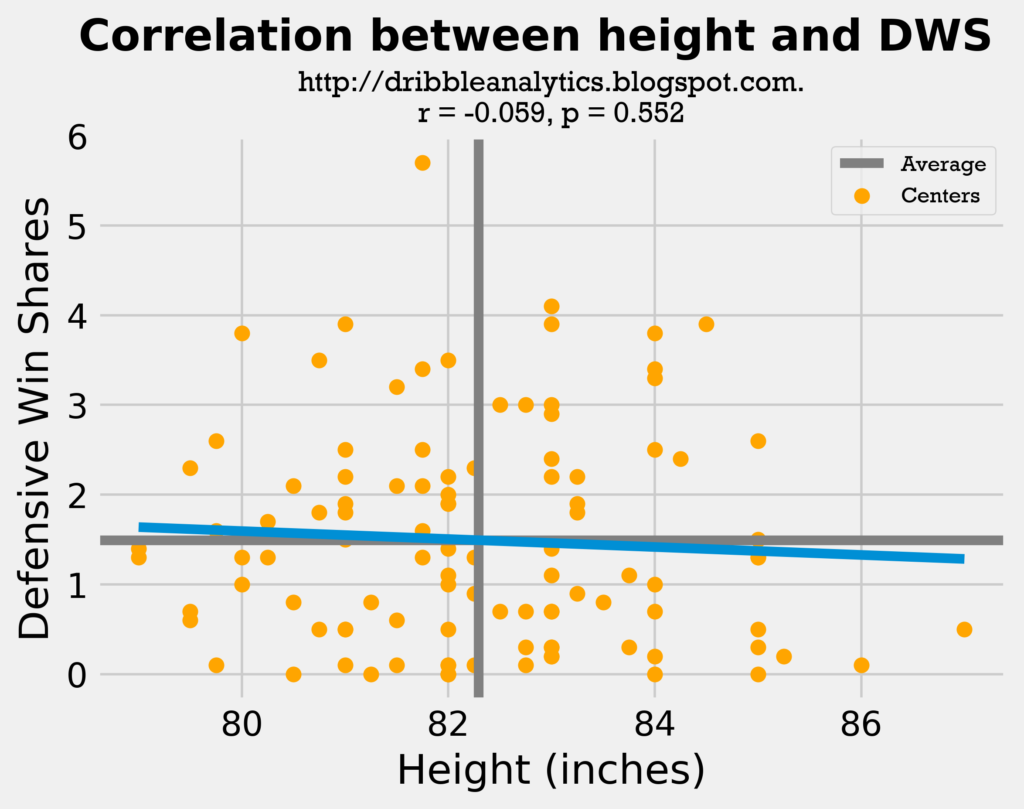
The correlation coefficient here for wingspan was the highest among any group, at 0.220. This result was also statistically significant, as it’s p-value was 0.024. Not only was the wingspan correlation coefficient high and significant, but also the height correlation coefficient was -0.059 with a p-value of 0.552. So, height had almost no correlation (essentially had a very minimal negative correlation) with DWS.The exponential trendline further demonstrates the importance of wingspan over height in this age of switching.

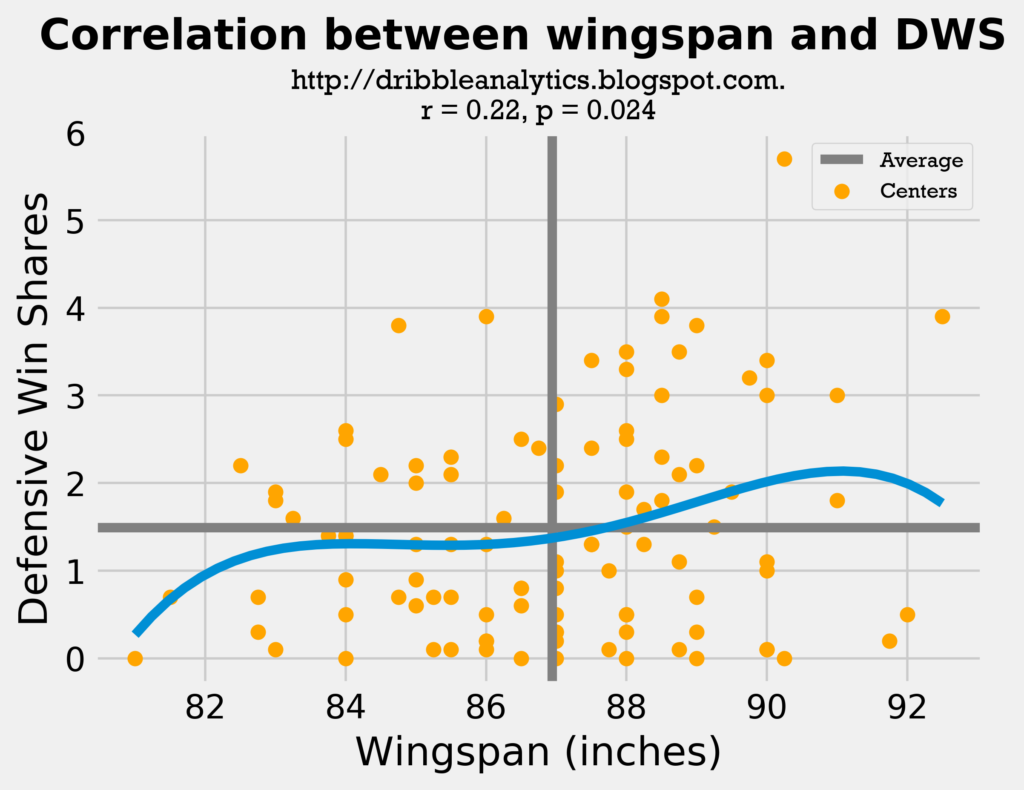
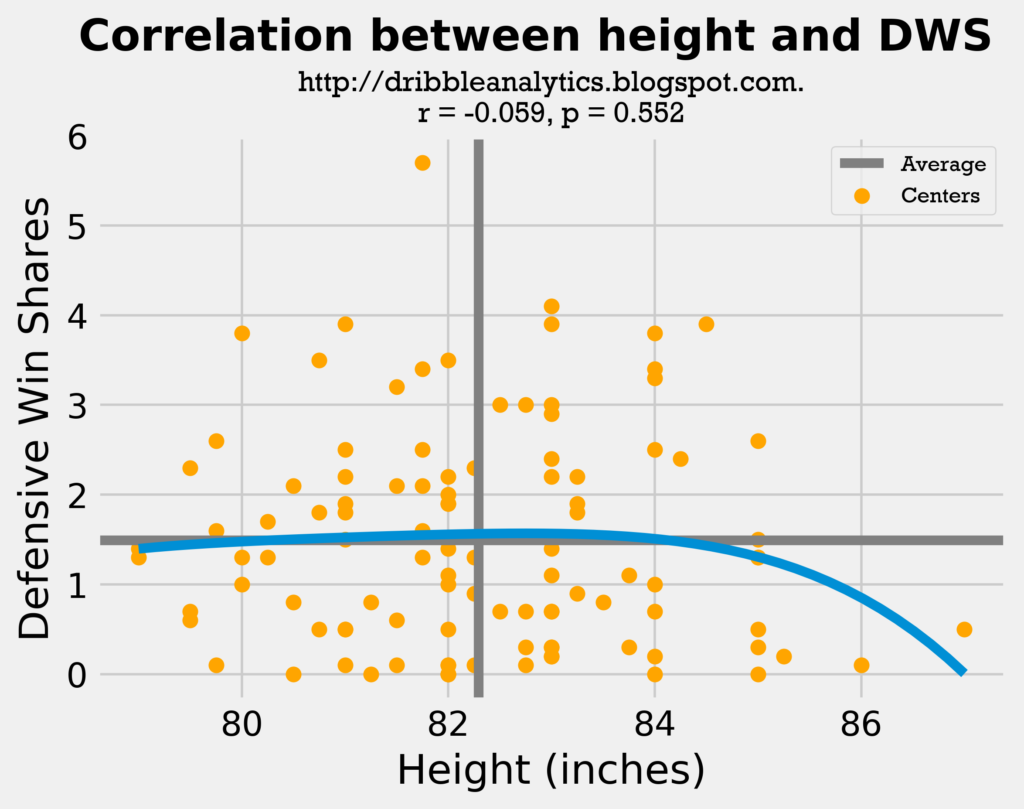
Both trendlines stay mostly consistent for the majority of the data. The wingspan trendline consistently rises, while the height trendline stays level. However, as the height approaches 7-footers, the trendline drops drastically. This is probably because at that point, the player is probably not very mobile, and therefore not as useful in today’s NBA on defense.

Summary:

• Wingspan: correlation coefficient = 0.220, p-value = 0.024 (statistically significant)
• Height: correlation coefficient = -0.059, p-value = 0.552 (not statistically significant)

Results: All NBA Teams

On a player-by-player basis, wingspan and height are clearly not the only factors influencing defense; effort, defensive ability, quickness, etc. probably influence defense more than measurements. On a team-by-team basis, these external factors are even larger. The factors considered include not only the individual player factors mentioned above, but also coaching, tanking, and coasting through the regular season (…Cavs).  

Because of these various external factors, the full team regressions are not as telling as the player regressions. Nevertheless, they do support the idea that wingspan is more important than height.

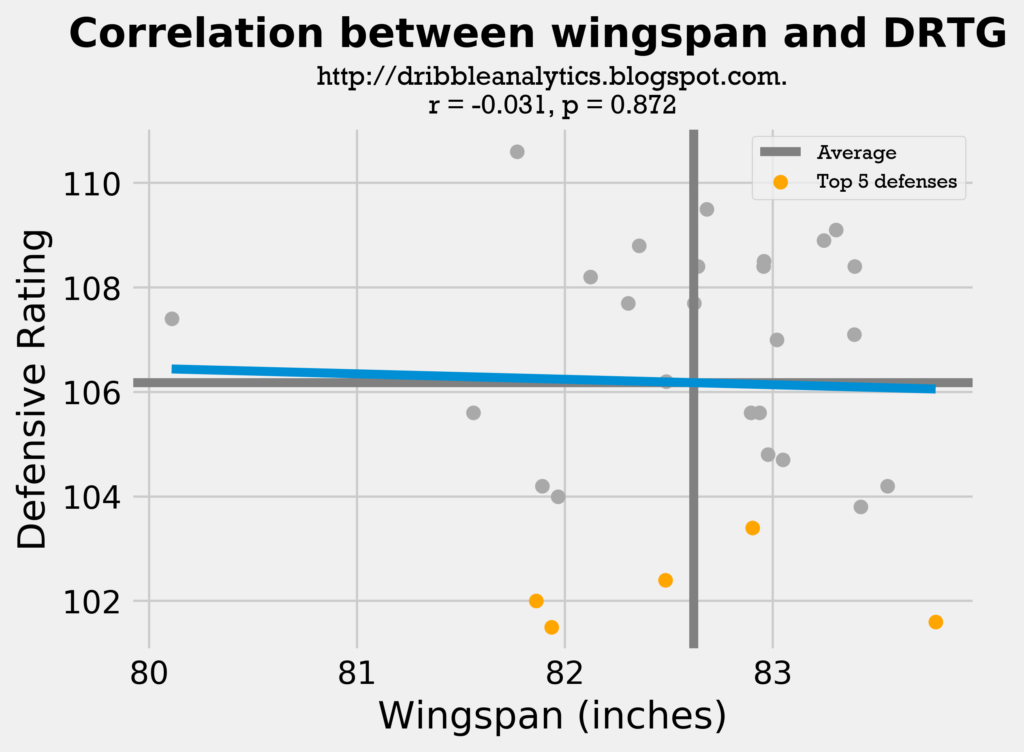
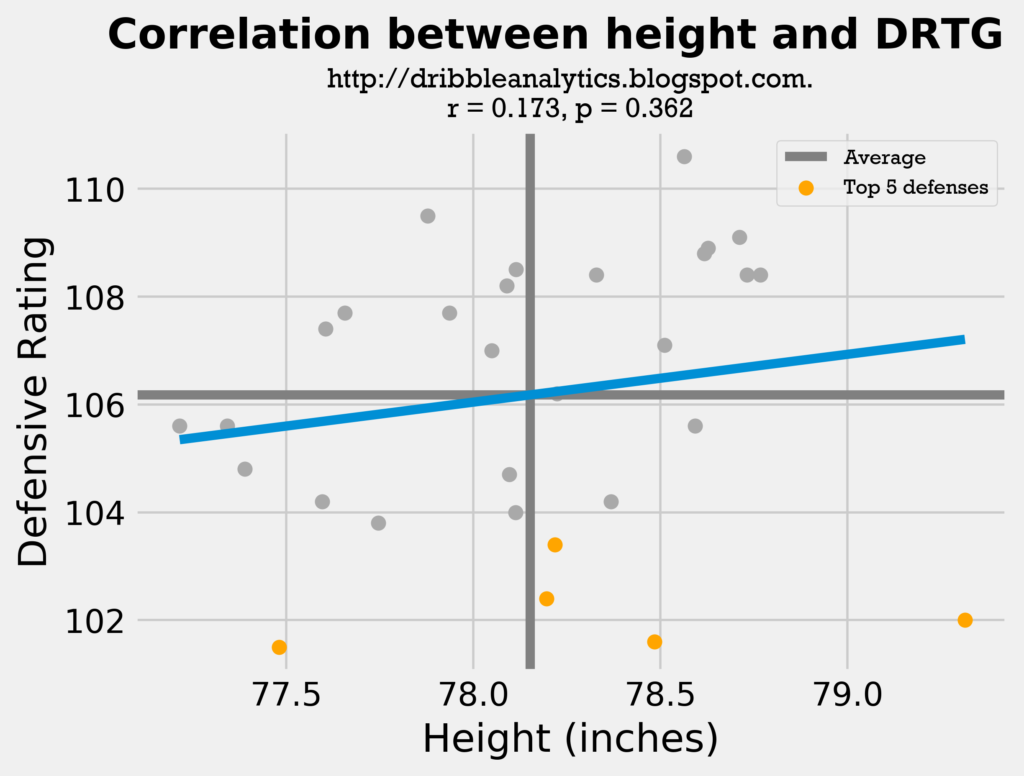
Here, the height correlation coefficient is much higher than the wingspan coefficient (0.173 vs. -0.031). A lower defensive rating is better, so a more positive correlation is worse. Both results are very far from statistical significance, as the wingspan p-value = 0.872, and the height p-value = 0.372. Also, 3 of the top 5 defensive teams have above-average heights, while only 2 of the top 5 defensive teams have above-average wingspans. So, even though the wingspan r-value is better, there isn’t a firm conclusion to be reached from the linear trendline.  

Though the r-values and p-values stay the same in the exponential trendline (so it’s still not significant), the trendline can give us some more context.

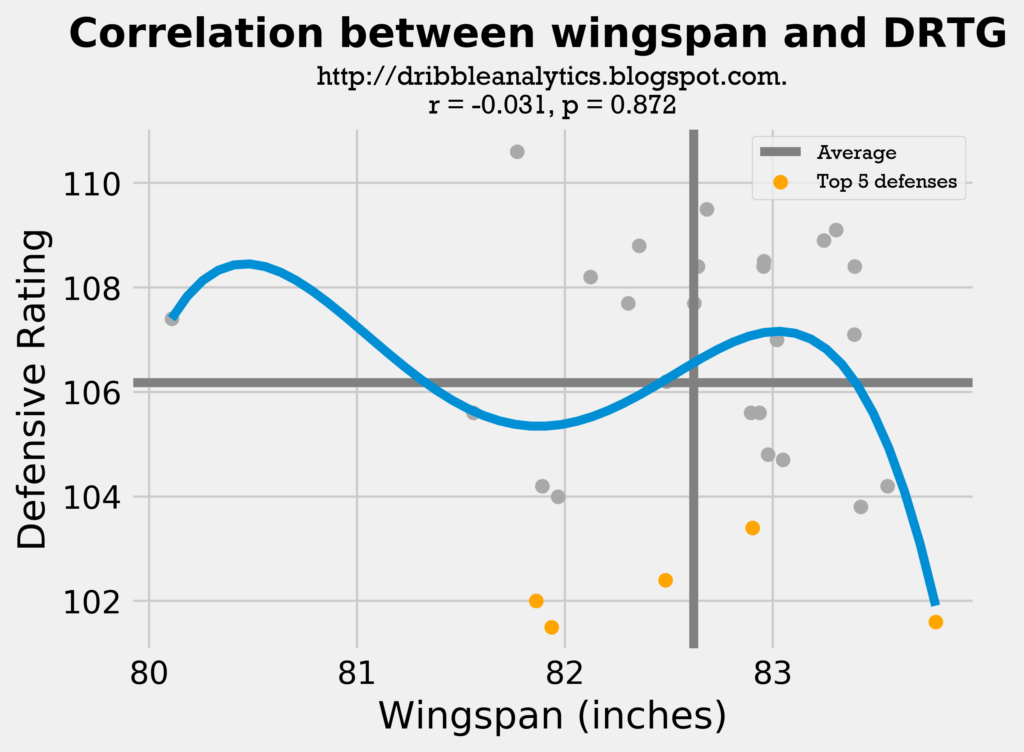
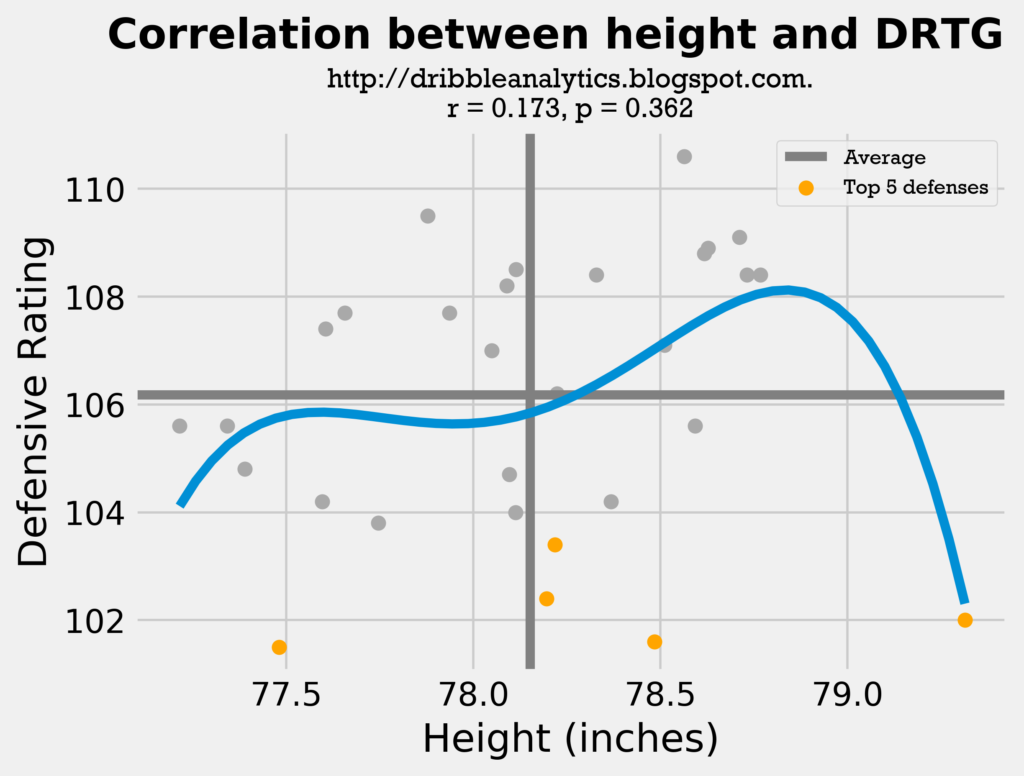
From these exponential trendlines, we can learn three things:

1. Even though the large rise in DRTG at the left-most end of the wingspan trendline is solely due to the Dallas Mavericks’ wingspan being much shorter, we can assume that teams with very short wingspans don’t have much defensive potential. The sharp drop at the right-most end indicates that teams with long wingspans probably have a lot of defensive potential.
2. At a near-average wingspan, the trendline fluctuates. This is probably due to the external factors mentioned. So, even if a team’s wingspan is close to the league’s average, it’s defense can still be bad.
3. Because the height trendline drops at both the right-most end and the left-most end, we can’t draw a conclusion about height like we did in point #1. A shorter team will not have less defensive potential than a longer team.

Summary (remember that a negative correlation coefficient is better, because a lower DRTG is better):

• Wingspan: correlation coefficient = -0.031, p-value = 0.872 (not statistically significant)
• Height: correlation coefficient = 0.173, p-value = 0.362 (not statistically significant)